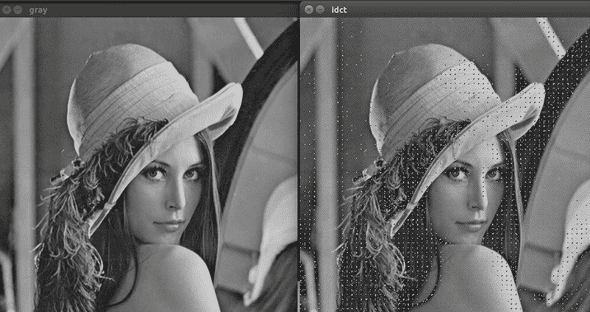
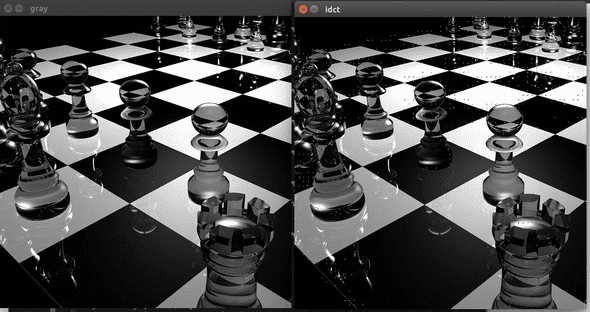
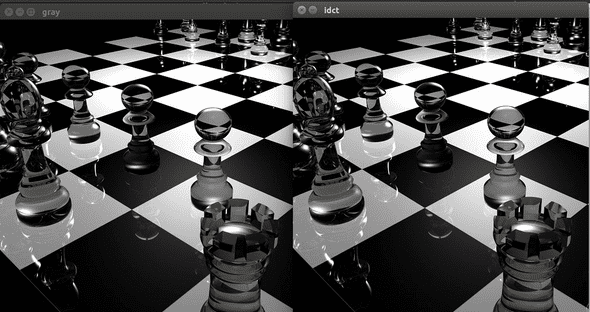
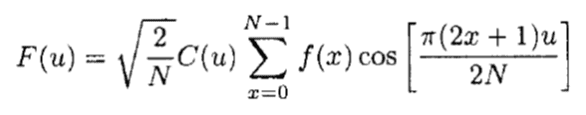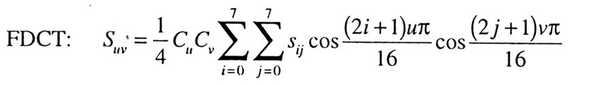IDCT图像压缩，Peak signal-to-noise ratio 实验
April 18, 2016
-
首先将其转为灰度图
def gray_scale(img): def gray_rgb(r, g, b): return (r*299 + g*587 + b*114) // 1000 gray = numpy.zeros((img.shape[0],img.shape[1]), dtype=img.dtype) for i in range(img.shape[0]): for j in range(img.shape[1]): gray[i,j] = gray_rgb(img[i,j,0], img[i,j,1], img[i,j,2]) return gray转换效果
-
1D-DCT 使用公式
def dct_1d(arr): def C(u): if u == 0: return 1 / math.sqrt(2) return 1 N = len(arr) res = numpy.zeros(N) for u in range(N): sum_var = 0 for x in range(N): sum_var = sum_var + arr[x] * math.cos(math.pi * (2 * x + 1) * u / (2 * N)) res[u] = math.sqrt(2.0/N) * C(u) * sum_var return res得到输出
first row [ 2.65134107e+03 -6.31674477e+01 6.20714540e+01 1.84602898e+02 -3.57774391e+01 2.34703032e+02 8.13877704e+01 -1.82167471e+00 ... -1.20049964e+00 -1.66465397e+00 -3.29829066e+00 -5.25334989e+00 -2.67329063e+00 4.89008657e-01 1.39333862e+00 -2.11832230e+00] first column [ 1.81779476e+03 5.97185841e+02 1.09031081e+02 1.90568707e+02 1.42346997e+02 9.85597307e+01 -6.97990414e+01 -8.49555225e+01 ... -1.54346100e+00 7.88274867e-01 7.52136601e-01 1.18425906e+00 -1.10638153e+00 -8.38384846e-01 -3.58717920e-01 -3.44971891e+00] -
在整个图片上使用 2D-DCT 使用公式
def dct_2d(arr): x = arr.shape[0] y = arr.shape[1] def C(u, v): if u == 0 and v == 0: return 1.0 / math.sqrt(2) return 1 res = np.zeros((x, y)) for u in range(x): for v in range(y): sum_var_x = 0 for i in range(x): sum_var_y = 0 for j in range(y): sum_var_y = (sum_var_y + arr[i,j] * math.cos((2*i + 1) * u * pi / (2 * x)) * math.cos((2*j + 1) * v * pi / (2 * y))) sum_var_x = sum_var_x + sum_var_y res[u,v] = 1/4 * C(u,v) * sum_var_x return res结果为
[[ 56100. 59925. 64005. ..., 0. 0. 0.] [ 2550. 2805. 61710. ..., 0. 0. 0.] [ 64770. 1785. 62985. ..., 0. 0. 0.] ..., [ 0. 0. 0. ..., 0. 0. 0.] [ 0. 0. 0. ..., 0. 0. 0.] [ 0. 0. 0. ..., 0. 0. 0.]]不过因为没有做优化，所以计算速度非常慢，大约半个小时以上。其实可以用先算系数矩阵然后矩阵相乘的方式改善代码
-
在
8*8块上使用 代码同上，选取最左上角的8*8块 结果为[[ 1020. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0.]] - 分析时间复杂度
从代码来看，时间复杂度为
O(u^2*v^2) -
PSNR after reconstruction by IDCT 首先实现IDCT
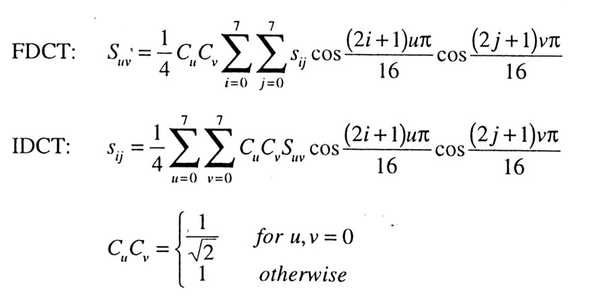在dct的基础上修改一下即可def idct_2d(arr): x = arr.shape[0] y = arr.shape[1] def C(u, v): if u == 0 and v == 0: return 1.0 / math.sqrt(2) return 1 res = np.zeros((x, y)) for u in range(x): for v in range(y): sum_var_x = 0 for i in range(x): sum_var_y = 0 for j in range(y): sum_var_y = C(i,j) * (sum_var_y + arr[i,j] * math.cos((2*u + 1) * i * pi / (0.1 * 2 * x)) * math.cos((2*v + 1) * j * pi / (0.1 * 2 * y))) sum_var_x = sum_var_x + sum_var_y res[u,v] = 1.0/4 * sum_var_x return res使用cv2.imshow看一下效果
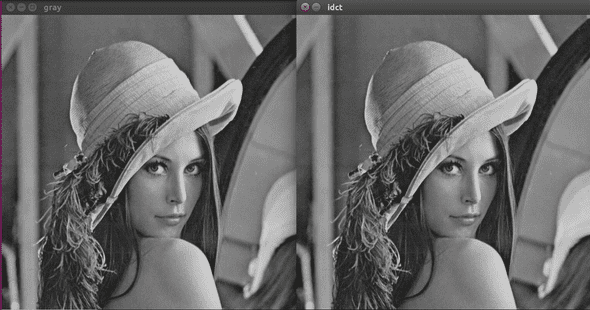
直接看的话，感觉没看出什么差别
计算一下PSNRdef psnr(img1, img2): def mse(imageA, imageB): err = np.sum((imageA.astype("float") - imageB.astype("float")) ** 2) err /= float(imageA.shape[0] * imageA.shape[1]) return err return 10 * math.log(255 ** 2 / mse(img1, img2))结果为
114.916476293相似度很高
-
What if only using 1/4,1/16, 1/64 DCT coefficients 为了方便，我直接选用了左上角的矩阵
-
当为1/4时，选取1/2,1/2的矩阵 按照上一步相同的步骤操作，得到图像
肉眼上没看出什么区别
计算一下psnr83.1366893938虽然肉眼没看出什么区别，不过psnr的值的确下降了一些
-
当为1/16时，选取1/4,1/4的矩阵 同上操作，得到图像
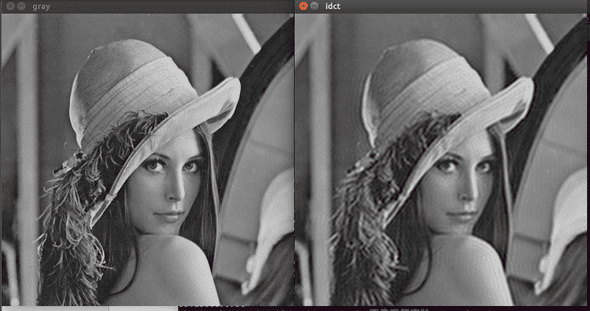肉眼已经可以明显看出区别了，idct后的图片明显要模糊一些
算一下psnr68.8003118691psnr有所下降，不过和上一步相比的话并不算多。只单纯从图像上看我还以为要降很多
-
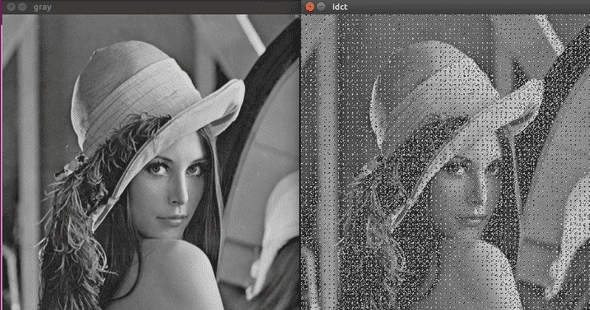
当为1/64时，选取1/8,1/8的矩阵 同上操作，得到图像
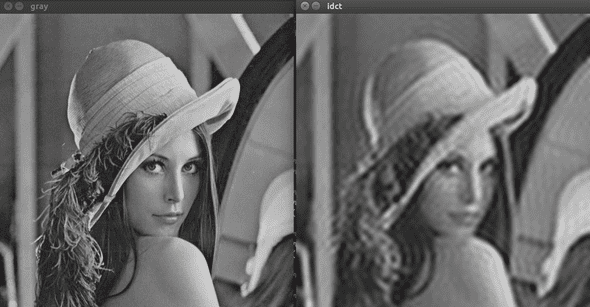这时差别已经非常明显了，右边的图像变的非常模糊，不过大致的轮廓都还很清楚。其实也应该是这样，因为左上角对于dct来说对应了低频部分，舍去了高频部分会丢失一些图像细节，不过大致轮廓还会显示出来
算一下psnr59.7402291887psnr有所下降，不过并不算多，意外的降得很少。或许psnr值与人眼的直接感受的敏感度有不少差别
-
为了方便，直接在之前的基础上修改代码
arr = np.float32(gray)
dst = np.zeros((512,512))
for i in range(512 // 8):
for j in range(512 // 8):
dst[i*8 : (i+1)*8, j*8 : (j+1)*8] = dct_2(arr[i*8:(i+1)*8,j*8:(j+1)*8])
...
idct = np.zeros((512, 512))
for i in range(512 // 8):
for j in range(512 // 8):
idct[i*8:(i+1)*8,j*8:(j+1)*8] = idct_2(dst[i*8:(i+1)*8,j*8:(j+1)*8],(8,8))
idct = idct * 255先生成一下图像看一下结果
好像哪里不对，psnr也只有19.2240715552，应该是代码bug。继续修改代码
arr = np.float32(gray) / 255.0
dst = np.zeros((512,512))
for i in range(512 // 8):
for j in range(512 // 8):
dst[i*8 : (i+1)*8, j*8 : (j+1)*8] = dct_2(arr[i*8:(i+1)*8,j*8:(j+1)*8])
...
idct = np.zeros((512, 512))
for i in range(512 // 8):
for j in range(512 // 8):
idct[i*8:(i+1)*8,j*8:(j+1)*8] = idct_2(dst[i*8:(i+1)*8,j*8:(j+1)*8],(8,8))
idct = idct * 255图像为
看来这样是正常了，看一下psnr
121.015204859比之前全局dct的时候还要高，虽然肉眼没看出什么区别
计算每一块的psnr，并计算平均值
psnr_list = []
for i in range(512 // 8):
for j in range(512 // 8):
temp_psnr = psnr(idct_res[i*8:(i+1)*8,j*8:(j+1)*8],gray[i*8:(i+1)*8,j*8:(j+1)*8])
psnr_list.append(temp_psnr)
print "i : ", i, " j : ", j, "psnr : ", temp_psnr
print "average psnr : ", sum(psnr_list) / len(psnr_list)结果为
i : 0 j : 0 psnr : 126.023528441
i : 0 j : 1 psnr : 114.127687772
i : 0 j : 2 psnr : 118.074229692
i : 0 j : 3 psnr : 117.756742709
i : 0 j : 4 psnr : 114.80210058
i : 0 j : 5 psnr : 134.496507044
i : 0 j : 6 psnr : 123.510384158
i : 0 j : 7 psnr : 126.023528441
i : 0 j : 8 psnr : 122.456779001
i : 0 j : 9 psnr : 127.565035239
i : 0 j : 10 psnr : 131.61968632
i : 0 j : 11 psnr : inf
i : 0 j : 12 psnr : 116.578912352
...
i : 63 j : 51 psnr : 125.333599726
i : 63 j : 52 psnr : 116.578912352
i : 63 j : 53 psnr : 115.525307196
i : 63 j : 54 psnr : 127.565035239
i : 63 j : 55 psnr : 123.510384158
i : 63 j : 56 psnr : 124.081968296
i : 63 j : 57 psnr : 111.983589058
i : 63 j : 58 psnr : 129.388250807
i : 63 j : 59 psnr : 114.127687772
i : 63 j : 60 psnr : 118.074229692
i : 63 j : 61 psnr : 141.42797885
i : 63 j : 62 psnr : 128.435149009
i : 63 j : 63 psnr : 131.61968632
average psnr : inf不过看来其中有inf，去除inf再次计算平均值
for i in range(512 // 8):
for j in range(512 // 8):
temp_psnr = psnr(idct_res[i*8:(i+1)*8,j*8:(j+1)*8],gray[i*8:(i+1)*8,j*8:(j+1)*8])
if temp_psnr != float('inf')
psnr_list.append(temp_psnr)
print "i : ", i, " j : ", j, "psnr : ", temp_psnr结果
average psnr : 123.177068712进行量化
Q = np.array([[16, 11, 10, 16, 24, 40, 51, 61],
[12, 12, 14, 19, 26, 58, 60, 55],
[14, 13, 16, 24, 40, 57, 69, 56],
[14, 17, 22, 29, 51, 87, 80, 62],
[18, 22, 37, 56, 68,109,103, 77],
[24, 35, 55, 64, 81,104,113, 92],
[49, 64, 78, 87,103,121,120,101],
[72, 92, 95, 98,112,100,103, 99]])
Q = 0.1 * Q
Q = Q / 255.0
arr = np.float32(gray) / 255.0
dst = np.zeros((512,512))
for i in range(512 // 8):
for j in range(512 // 8):
dst[i*8 : (i+1)*8, j*8 : (j+1)*8] = dct_2(arr[i*8:(i+1)*8,j*8:(j+1)*8]) // Q * Q看一下效果
好像不怎么好
psnr为
31.0463837901
average psnr : 32.0848558543使用 a*Q 量化，使a=0.1时
看起来不错，肉眼没看出什么差别
对于psnr
80.2997218444
average psnr : 80.453595816使a=0.5
图像开始不清晰
psnr为
43.7616530849
average psnr : 45.26357418使a=0.3
psnr为
55.4620216976
average psnr : 57.1084289312感觉细节丰富的地方容易产生不清晰，可能是因为高频信息被量化的比较狠的缘故，或者是代码bug
现在看来还是a = 0.1时最好，量化矩阵可以取a*Q，适当减轻了高频信息，保留低频信息，并且也不显得整体模糊
对于别的图片进行尝试
psnr
62.1518847038
average psnr : 107.223096725细节地方还是有些模糊，继续调节
psnr为
119.861063688
average psnr : 118.77862201全局psnr忽然就升了上来，已经很清晰了